MAŠINŲ IR MECHANIZMŲ TEORIJA

Ištrauka

MAŠINŲ IR MECHANIZMŲ TEORIJA 
KURSINIS PROJEKTAS

TURINYS
1. ĮVADAS………………………. …………………………………………3
1.1 UŽDUOTIES LAPAS……………………………………………………… 4
2. SVIVRTINIO MECHANIZMO PROJEKTAVIMAS …………….. ………… ..5
2.1. Laisvės laipsnių skaičius……………………………………………………………… ….5
2.2. Metrinė sintezė………………………………………………………………………… ….6
2.3. Kinematinė analizė…………………………………………………………………… … 7
3. KUMŠTELIO MECHANIZMO PROJEKTAVIMAS …………………… ……17
3.1. Pradiniai duomenys…………………………………………………………………… …17
3.2. Kumštelio projektavimas……………………………………………………………… …18
3.3. Kumštelio mechanizmo duomenys…………………………………………………… ….20
4. KRUMPLIARAČIO MECHANIZMO PROJEKTAVIMAS ……………… ….27
4.1. Krumpliaračių duomenų skaičiavimas………………………………………………… …28
4.2 Krumpliaračių sankiba…………………………………………… ……………………….35 
4.3. Planetinio reduktoriaus projektavimas………………………………………………… 37
5. SMAGRAČIO PROJEKTAVIMAS ………………………………………… 40
5.1 Redukuotojo inercijos momento nustatymas…………………………………………….40
5.2 Smagračio projektavimas…………………………………………………………………52

ĮVADAS
Kursinis projektas susideda iš keturių etapų – pirmiausiai suprojektuojamas svirtinis
mechanizmas.
Nustatomas šio mechanizmo laisvės laipsnis, klasė ir eilė. Taip sužinoma kokio sudėtingumo
yra mechanizmas. Toliau atliekama jo kinematinė analizė.
Antrajame etape atliekamas kumštelinio mechanizmo projektavimas.
Trečioje dalyje projektuojama dviejų krumpliaračių sankiba bei planetinis reduktorius.
Projektas baigiamas smagračio projektavimu visai mašinai pagal užduotą jos eigos netolygumo
koeficientą.

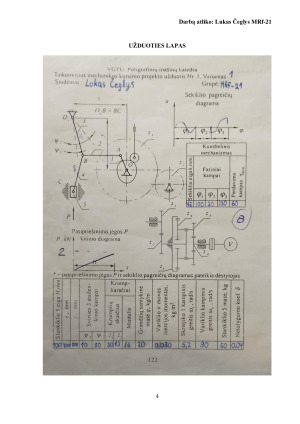
UŽDUOTIES LAPAS

SVIRTINIO MECHANIZMO PROJEKTAVIMAS

2.1 Laisvės laipsnių skaičiavimas
Mechanizmo projektavimas prasideda nuo susipažinimo su juo, t.y. mechanizmo laisvės
laipsnis – taiskaičius grandžių, nuo kurių priklauso viso mechanizmo judesiai, tuo pačiu
parodantis, keliomis apibendrintomis koordinatėmis jį galima aprašyti. Klasė ir eilė parodo,
kokio sudėtingumo yra mechanizmas ir kokius tyrimo metodus reikės taikyti. Mechanizmo
laisvės laipsnis apskaičiuojamas pagal formulę:
W= 3n - 2p5 - p4;
Čia W - mechanizmo laisvės laipsnis,
n - judančių grandžių skaičius,
5p - penktos klasės kinematinių porų skaičius,
4p - ketvirtos klasės kinematinių porų skaičius ( pagal Artobolevskio klasifikaciją).
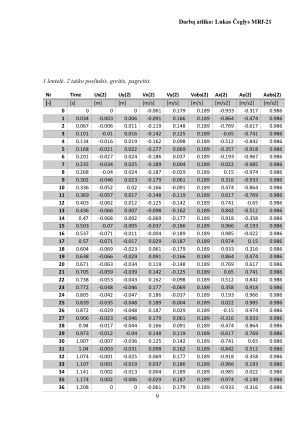
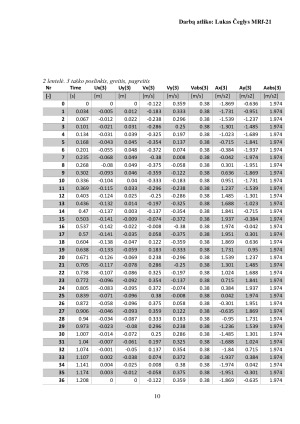
Tiriamo mechanizmo laisvės laipsnio paskaičiavimas:
W= 35-27-0 =1
Rastas laisvės laipsnis parodo, kad viso mechanizmo
judesys priklauso nuo vienos grandies, šiuo atveju nuo
pirmosios (skriejiko) grandies, ji vadinama varančiąja, ir
bet kurią mechanizmo padėtį galima aprašyti vienu kintamuoju.
Klasė ir eilė nustatoma išskaidžius mechanizmą
į Asūro grupes. Pagal aukščiausią Asūro grupės klasę ir
eilę sprendžiama, kad nagrinėjamas mechanizmas yra 2
klasės ir 4 eilės. Tai reiškia, kad braižydami greičių ir
pagreičių planus naudosimės paprastomis greičių ir
pagreičių braižymo lygtimis.