Kiekybinių sprendimų metodai

Ištrauka

Kursinis darbas
Kiekybinių sprendimų metodai

Turinys
Įvadas 3
1. Koreliacinė regresinė analizė 4
1.1 Tyrimo tikslai 4
1.2 Koreliacinė analizė Y su kiekvienu X1, , X5 5
1.3 Atrinkti X1,…, X5 regresinei analizei atlikti 6
1.4 Porinė regresinė analyze Y su kiekvienu X3, X4, X5 6
1.5 Daugianarė koreliacinė regresinė analizė 10
1.6 Gautų rezultatų aprašymas 12
1.7 Tyrimo rezultatų taikymo pavyzdžiai 12
2. Prognozavimas 13
2.1 Slenkančio vidurkio metodas 13
2.2 Eksponentinis išlyginimo metodas 14
3. Gamybos planavimo uždavinys 15
3.1 Gamybos planavimo uždavinio sudarymas ir grafinis jo sprendimas 15
3.2 Uždavinio sprendimas su SOLVER pagalba 17

Įvadas
Šiuolaikinėje nuolat besivystančioje visuomenėje susiduriame su itin skirtingomis ir viena nuo
kitos priklausančiomis problemomis. Pasiekti vieną svarbų aspektą reikia tobulinti daugybę kitų.
Kadangi paprastam žmogui yra sunku suvokti kas nuo ko priklauso, nes priimami sprendimai lemia
vis didesnį vaidmenį skirtingose srityse, šalia tradicinės ekonomikos ir valdymo metodų labai greitai
pradėjo plisti vis naujų kiekybinių metodų. Šie metodai leidžia naudotis kompiuteriais ir funkcijomis
uždaviniams išspręsti.
Šio kursinio darbo tikslas yra išnagrinėti pasirinktus kintamuosius, t.y. kas lemia restorano
“Fortas” lankytojų skaičių per metus. Todėl ieškosiu ryšių atlikdama koreliacinę analizę, porinę
koreliaciją, porinę regresiją ir daugianarę regresiją. Taip pat atliekant slenkančio vidurkio ir
eksponentinio išlyginimo metodus.

1. Koreliacinė regresinė analizė
1.1 Tyrimo tikslai
Koreliacinė regresinė analizė dažnai yra taikoma, kai reikia nustatyti, ar egzistuoja stochastinis
(atsitiktinis) ryšys tarp nagrinėjamų veiksnių. Šio kursinio darbo tikslas yra atlikti koreliacinę
regresinę analizę ir nustatyti, ar egzistuoja stochastinis ryšys tarp veiksnių Y ir X, ir tarp kurių
veiksnių egzistuoja funkcinė priklausomybė.
Tyrimo tikslai:
1.1.Nustatyti, kaip Y (lankytojų skaičius per metus) įtakoja tokie veiksniai kaip:
a) Darbuotojų skaičius (X1);
b) Staliukų skaičius (X2);
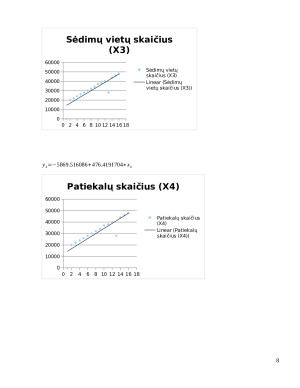
c) Sėdimų vietų skaičius (X3);
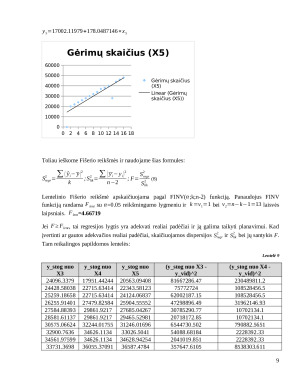
d) Patiekalų skaičius (X4);
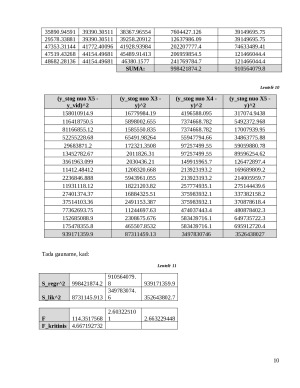
e) Gėrimų skaičius (X5);
1.2. Nustatytį ryšių stiprumus, formą bei analitines išraiškas;
1.3. Nustatyti ryšių stiprumą tarp Y ir įtakingiausių veiksnių bei rasti tų ryšių formas ir analitines išraiškas;
1.4. Išrinkti kreivę, kuri geriausiai atvaizduotų statistinių taškų visumą ir nustatyti jos adekvatumą realiai padėčiai;
1.5. Aprašyti gautus rezultatus ir pateikti išvadas.