DIFERENCIALINIŲ LYGČIŲ MODELIAVIMAS

Ištrauka

2 laboratorinis darbas
DIFERENCIALINIŲ LYGČIŲ MODELIAVIMAS

Darbo tikslas: Susipažinti su diferencialinių lygčių modeliavimu, jų sprendinių ir
sprendinių dedamųjų paieška bei identifikavimu.
Teorinė dalis: Kiekvienos fizinės sistemos (proceso) valdymas yra susijęs su veikme jos
elgsenai, pagal nustatytą dėsnį keičiant užduoties (išorinį) poveikį. Norint suformuoti tinkamą
bet kurios sistemos valdymo dėsnį, pirmiausia reikia gauti duomenų apie jos elgseną. Šie
matematine išraiška pateikti duomenys – sistemos matematinis modelis – yra jos valdymo
vyksmo tyrimo pagrindas.
Kaip laikui bėgant keičiasi sistemos (proceso) elgsena, nustatoma matuojant jos reakciją.
Modelyje šis kitimas paprastai išreiškiamas diferencialine lygtimi arba diferencialinių lygčių
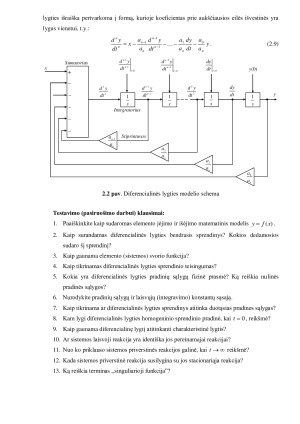
sistema. Sistema (procesas) (2.1 pav.), reaguodama į užduoties poveikį )(tx , generuoja reakciją )(ty. Jeigu poveikis )(tx yra apibrėžta laiko funkcija, tai poveikio ir reakcijos tarpusavio
priklausomybė )(xfy išreiškiama diferencialine lygtimi (arba diferencialinių lygčių sistema),
kurios bendrasis sprendinys – sistemos bendroji reakcija )(ty – yra laiko funkcija.
Kai sistemos matematinis modelis yra aprašytas diferencialine lygtimi, tai kitas žingsnis,
tiriant jos valdymo vyksmą, turėtų būti šios diferencialinės lygties sprendimas (integravimas) ir
rastojo sprendinio panaudojimas sistemos elgsenai prognozuoti.